本文共 935 字，大约阅读时间需要 3 分钟。

1. FFT

1. FFT：

   快速傅里叶变换（Fast FourierTransform）是离散傅立叶变换（DFT）的高速算法，能够将一个信号时域变换到频域。Why：有些信号在时域上是非常难看出什么特征的，可是如果变换到频域之后，就非常easy看出特征了。这就是非常多信号分析採用FFT变换的原因。另外，FFT能够将一个信号的频谱提取出来，这在频谱分析方面也是经经常使用的。

2. FFT物理意义：

   一个模拟信号，经过ADC採样之后，就变成了数字信号。採样定理告诉我们，採样频率要大于信号频率的两倍（定理）。採样得到的数字信号，就能够做FFT变换了。N个採样点，经过FFT之后，就能够得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。

如果採样频率为Fs，信号频率F，採样点数为N。那么FFT之后结果就是一个为N点的复数（e.g., a+bi）。对于第n个点：

如果原始信号的峰值为A，那么FFT的结果的每一个点（除了第一个点直流分量之外）的模值就是A的N/2。

3. 傅里叶公式：非周期性连续时间信号x(t)的傅里叶变换可以表示为：
   
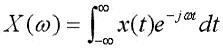   有限长离散信号x(n)，n=0，1，…，N-1的DFT定义为：
   
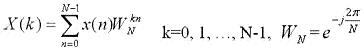   将x(n)分解为偶数与奇数的两个序列之和，即
   
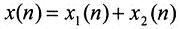   x1(n)和x2(n)的长度都是N／2，x1(n)是偶数序列，x2(n)是奇数序列，则
   
   其中X1(k)和X2(k)分别为x1(n)和x2(n)的N／2点DFT。由于X1(k)和X2(k)均以N／2为周期，且WN k+N/2=-WN k，所以X(k)又可表示为：
   
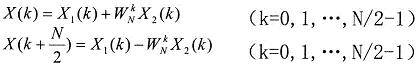
4. 原理
   快速傅里叶变换（Fast Fourier Transform，FFT）是一种可在 [公式] 时间内完成的离散傅里叶变换（Discrete Fourier transform，DFT）算法。

在算法竞赛中的运用主要是用来加速多项式的乘法。

需搞明白的概念：多项式表达式、点值表达式、复数、复数的单位根（傅里叶变换里用到的概念，有折半引理、和消去引理）

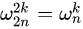
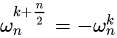
2. 信号滤波

什么是卷积？参考了知乎名嘴：

3. 相关

转载地址：http://rtiyk.baihongyu.com/